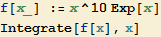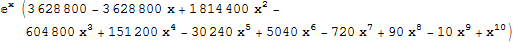3.2 Integrace per partes
Teorii naleznete v kapitole 6.2 Multimediální encyklopedie nebo v kapitole 3.2 Breviáře
Příklad 1
Pomocí metody per partes vypočítejte ∫ lnx dx.
Řešení
Obecný vzorec pro výpočet integrálu metodou per partes zní: ∫ f´(x)g(x)dx = f(x)g(x) - ∫ f(x)g´(x)dx.
V tomto případě, pokud chceme vypočítat integrál bez použití software, se integrand lnx upravuje na 1·lnx. Volíme f´(x) = 1, g(x) = lnx. Odtud plyne (jedná se o integrály elementárních funkcí, které by měl každý matematik znát zpaměti), že f(x) = x a g´(x)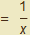 
. Pokud nyní použijeme větu per partes, održíme ∫ lnx dx = ∫ 1·lnx dx = x lnx - ∫1dx = x lnx - x + C.
Tento příklad je jednoduchý, přesto již vyžaduje jistou zkušenost v úpravě integrandu a volbě, kterou funci budeme integrovat a kterou derivovat (Opačná volba funkcí, tzn. f´(x) = lnx a g(x) = 1, by nám nepomohla, protože pro dosazení do věty per partes musíme vypočítat f(x)= ∫ f´(x)dx = ∫ lnx dx. )
Při výpočtech v Mathematice nám tyto (byť v tomto případě malé) obtíže odpadají, software vše spočte za nás.
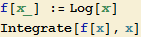
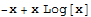
Příklad 2
Pomocí metody per partes vypočítejte ∫ x sinx dx.
Řešení
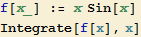
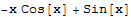
Příklad 3
Pomocí metody per partes vypočítejte ∫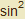 
x dx.
Řešení
Výpočet tohoto integrálu "vlastními silami" je komplikovanější, integrand je nutno rozložit na sinx · sinx a dále použít vztah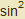 
x +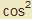
x = 1. Při použití software je vše jednodušší:
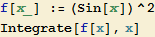
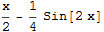
Příklad 4
Pomocí metody per partes vypočítejte ∫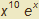 
dx.
Řešení
Kdybychom chtěli vypočítat tento integrál vlastními silami, byla by to časově náročná úloha. U tohoto příkladu je nutno použít metodu per partes celkem desetkrát za sebou (výpočet obdobného příkladu je uveden v Breviáři na straně 39, využívá se zde rekurentních vzorců)
